Posted on 2013-02-23 22:25
魔のkyo 阅读(4617)
评论(0) 编辑 收藏 引用

根据复数表示平面向量旋转在圆周上的线性插值可以推广得到四元数球面线性插值的公式
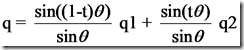
具体公式推导过程可以参考 Fletcher Dunn&Ian Parberry. 3D数学基础图形与游戏开发. P154~P157. 清华大学出版社
如果用四元数表示物体旋转,或者确切的说用四元数表示物体的角位置(旋转一词比较模糊可以视为过程量也可以视为状态量),如果想得到两个关键帧之间的角位置就可以使用四元数球面线性插值来得到中间的状态量,然而在实际使用中我发现根据上述公式计算的中间状态量并不总是沿着感觉上最小的转动方式进行转动的。
后来调查了一下发现这种情况放生在旋转轴方向相反时(确切的说是两个插值的四元数的转动轴夹角大于90°)
考虑到四元数q和-q表示的旋转其实的相同的,而所用的转动轴是反向的,所以当插值的的两个元素q1,q2的转动轴夹角大于90°时,其实可以用-q1代替q1或-q2代替q2再用上面的公式进行插值就可以避免这个问题。
直接给出整理优化后的四元数插值代码
template<typename Real>
Quaternion<Real> Slerp(const Quaternion<Real>& x, const Quaternion<Real>& y, Real lambda)
{
Real s = Length(x) * Length(y);
if(s < FLOAT_EPS)
return x;
Real fCos = Dot(x, y) / s;
if (Abs(fCos) >= 1.0f)
return x;
Real sign = (fCos < 0) ? -1.0f : 1.0f;
Real fAngle = Acos(sign * fCos);
Real fInvSin = 1.0f / Sin(fAngle);
Real fCoeff0 = Sin((1.0f - lambda) * fAngle);
Real fCoeff1 = Sin(sign * lambda * fAngle);
return (x * fCoeff0 + y * fCoeff1) * fInvSin;
}
PS:这里没有处理x,y恰好反向的情况。